Questo articolo ha il compito di risolvere il problema di come muovere gli elementi del gioco nella giusta direzione.
Nelle precedenti lezioni abbiamo disegnato l’Astronave e abbiamo visto come ruotarla nello spazio. Adesso vedremo come farla andare nella direzione giusta.
La nostra Astronave è posizionata su un piano di coordinate, per spostare questo elemento sarà sufficiente modificare il valore delle sue Proprietà x e y.
Il calcolo dei valori di x e y per muovere l’astronave coinvolge fondamentalmente due valori: la velocità e l’angolo di rotazione.
- La velocità l’abbiamo già prevista, anche se il suo valore è ancora impostato a zero.
- L’angolo lo conosciamo già perché lo abbiamo utilizzato per far ruotare l’astronave.
Gestione della velocità
La velocità sarà rappresentata da un numero, se l’utente premerà il tasto freccia su sulla tastiera questo valore aumenterà, altrimenti diminuirà gradualmente fino a tornare a zero.
Questo controllo va inserito nel Metodo goOn che abbiamo già all’interno della Classe AsteroidsGame:
private function goOn(e:TimerEvent) {
if (_keyDown[39]) {
_p.ruota('orario');
} else if (_keyDown[37]) {
_p.ruota('antiorario');
}
if (_keyDown[38]) {
_p.speed++;
} else {
_p.speed--;
}
_p.muovi();
}
L’Oggetto _keyDown è già predisposto per memorizzare tutti i codici dei tasti premuti sulla tastiera, nel codice che abbiamo aggiunto non facciamo altro che incrementare il valore di una Proprietà dell’Istanza di Player (_p.speed++) quando il tasto freccia su (codice 38) è premuto, e decrementarlo in caso contrario.
La Proprietà speed non esiste ancora nella Classe Player, esiste una Proprietà chiamata _speed ma è Privata, quindi dobbiamo inserire un Getter e un Setter per questa Proprietà. Dentro Player.as aggiungiamo queste due funzioni:
public function get speed():int {
return _speed;
}
public function set speed(s:int) {
if (s >= 0) {
_speed = s;
}
}
Adesso il valore di _speed è gestito, lo utilizzeremo più tardi.
Un po’ di trigonometria
Sono certo di aver perso il 99% dei lettori solo per aver utilizzato la parola “trigonometria”, ma andiamo avanti…
Il problema più grande che dobbiamo affrontare (e che ho provato a rimandare fino a questo momento) è quello si stabilire il valore delle Proprietà x e y dell’Astronave, in funzione dell’angolo di rotazione. Se l’Astronave si muovesse soltanto in quattro direzioni il problema sarebbe di facile soluzione:
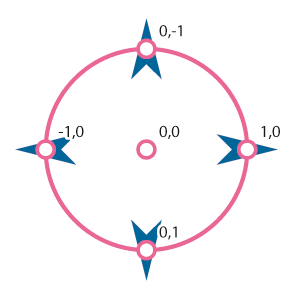
Noi dobbiamo essere in grado di calcolare i valori di spostamento orizzontale e verticale per ben 36 rotazioni diverse (da 0 a 360 con incremento di 10), e i numeri non sono così semplici:
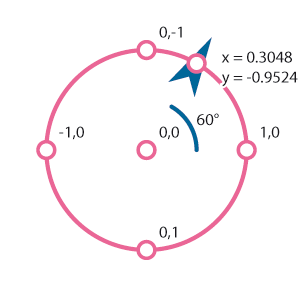
L’unico modo che abbiamo per calcolare le coordinate in questo caso è quello di ricorrere alle funzioni trigonometriche di Seno e Coseno.
La buona notizia è che possiamo contare sulle comodissime funzioni Math.sin e Math.cos per calcolare i valori di seno e coseno che ci servono. La cattiva notizia è che per utilizzare queste due funzioni dobbiamo convertire il valore di rotazione da Gradi Sessagesimali (valori da 0 a 360), che è l’unità di misura che stiamo usando, a Radianti (valori da 0 a 2π).
Per convertire questo valore ci serviremo di una semplice funzione:
public function g2r(gr:Number):Number {
return gr*Math.PI/180;
}
Questa funzione accetta un valore espresso in Gradi e restituisce il valore corrispondente in Radianti.
La funzione Muovi
Adesso che abbiamo tutto quello che ci serve possiamo finalmente scrivere la funzione che muove l’Astronave e vedere qualche risultato:
public function muovi() {
this.x += Math.cos(g2r(this.rotation-90))*_speed;
this.y += Math.sin(g2r(this.rotation-90))*_speed;
this.x = this.x < 0 ? stage.stageWidth : this.x > stage.stageWidth ? 0 : this.x;
this.y = this.y < 0 ? stage.stageHeight : this.y > stage.stageHeight ? 0 : this.y;
}
Questa funzione utilizza i Metodi sin e cos per calcolare lo spostamento x e y dell’Astronave in base all’angolo di rotazione, successivamente controlla se lo Sprite è uscito fuori dallo schermo per riportarlo dentro al quadro. Il risultato di questa lezione è questo:
[kml_flashembed publishmethod=”dynamic” fversion=”10.0.0″ useexpressinstall=”true” movie=”https://www.danielealessandra.com/wp-content/uploads/2010/04/Asteroids1.swf” width=”300″ height=”300″ targetclass=”flashmovie”]
[/kml_flashembed]
Il movimento non è ancora soddisfacente e spero che questa lezione non vi abbia spaventato tanto da impedirvi di seguire le lezioni successive.


3 replies on “Realizzare Asteroids [parte 3]”
Ciao ,
sto prendendo spunto dalla tua guida per creare un mio videogioco.
Ce` una cosa che non capisco, perche` nella funzioni muovi sottrai 90 dal valore di rotation?
this.x += Math.cos(g2r(this.rotation-90))*_speed;
potresti spiegarmi??
grazie andrea
Certo, è molto semplice…
quando ho disegnato l’astronave l’ho fatta con la punta rivolta verso l’alto, invece l’angolo zero è rivolto verso destra; quindi il disegno dell’astronave si trovava ruotato di 90° rispetto al sistema di riferimento.
Per questo motivo avrei dovuto ridisegnare l’astronave in modo che all’inizio puntasse verso destra, oppure sottrarre 90 gradi alla rotazione, e così ho fatto… non mi andava di tornare a correggere un articolo già pubblicato.
Grazie per aver letto il mio blog, torna a trovarmi :)
Grazie Daniele,
mi ha preceduto di qlc secondo ero andato a rivedere la parte dove disegnavi l`astronave e vedendo i tuoi disegni ci ero arrivato.
Non sai quanto e` utile il tuo tutorial grazie.